Skip to main content
Version: 4.x

Indexing

H3 is a hierarchical geospatial index. H3 indexes refer to cells by the spatial hierarchy. Every hexagonal cell, up to the maximum resolution supported by H3, has seven child cells below it in this hierarchy. This subdivision is referred to as aperture 7.


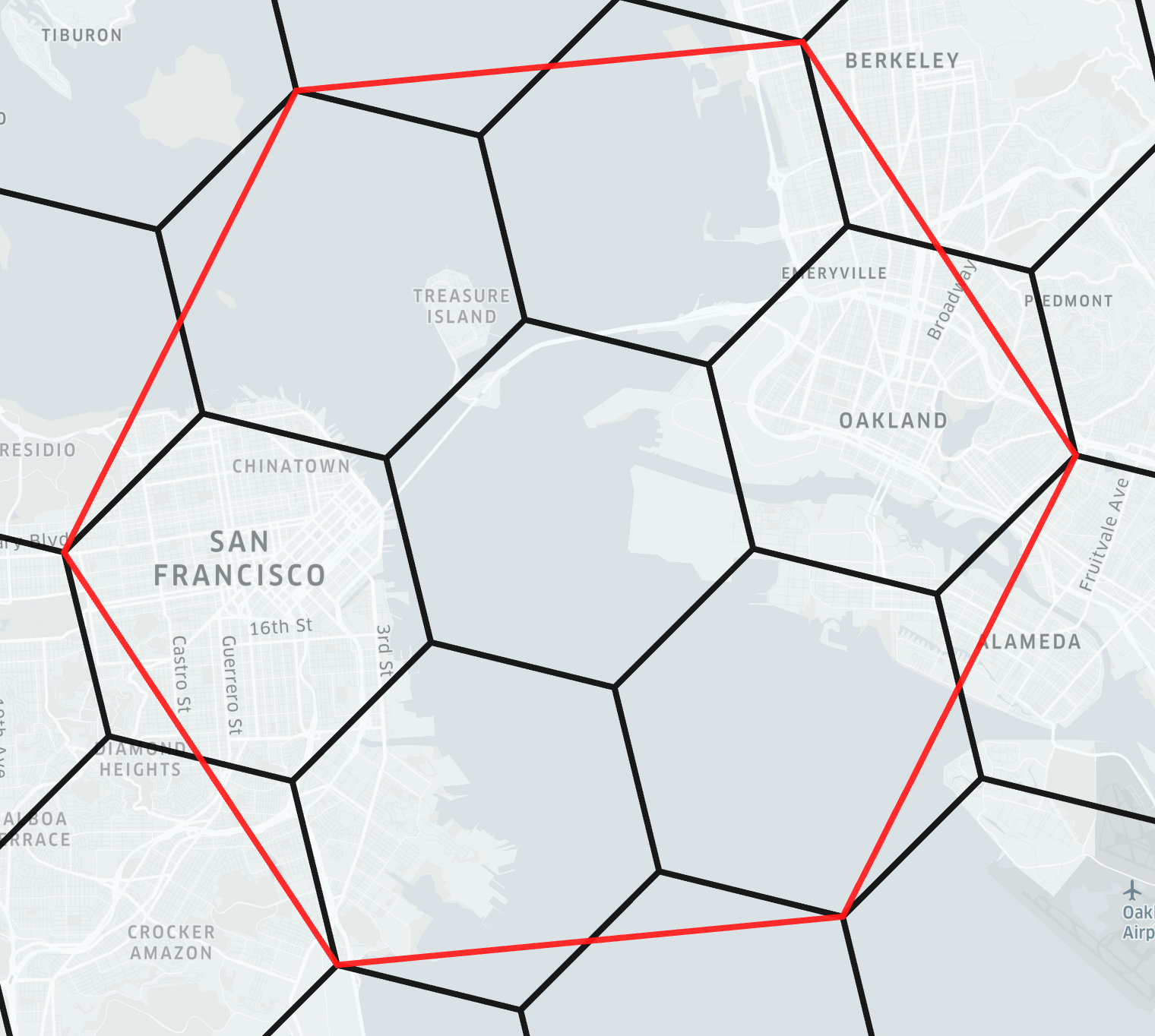
A parent hexagon approximately contains seven children

Hexagons do not cleanly subdivide into seven finer hexagons. However, by alternating the orientation of grids a subdivision into seven cells can be approximated. This makes it possible to truncate the precision within a fixed margin of error of an H3 index. It is also possible to determine all the children of a parent H3 index.

Approximate containment only applies when truncating the precision of an H3 index. The borders of hexagons indexed at a specific resolution are not approximate and not affected by these considerations. For example, indexing points to cells at a certain resolution and finding those cell's neighbors is not affected by approximate containment.

While geographic containment is approximate, logical containment in the index is exact. It is possible to use H3 as an exact logical index on top of data indexed at a specific resolution.

This approximation allows for efficiently relating datasets indexed at different resolutions of the H3 grid. The functions for changing precision (h3ToParent, h3ToChildren) are implemented with only a few bitwise operations, making them very fast. The structure of the H3 index means that geographically close locations will tend to have numerically close indexes.

The hierarchical structure can also be used in analysis, when the precision or uncertainty for a location needs to be encoded in the spatial index. For example, a point from a GPS receiver could be indexed at a coarser resolution when the precision of the signal is lower, or some cells could be aggregated to a parent cell when there are too few data points in each of the finer cells.

Hierarchical containment allows for use cases like making contiguous sets of cells "compact" with compactCells. It is then possible to uncompactCells to the same input set of cells, or to test whether a cell is contained by the compact set.

Uncompacted (dense)Compacted (sparse)
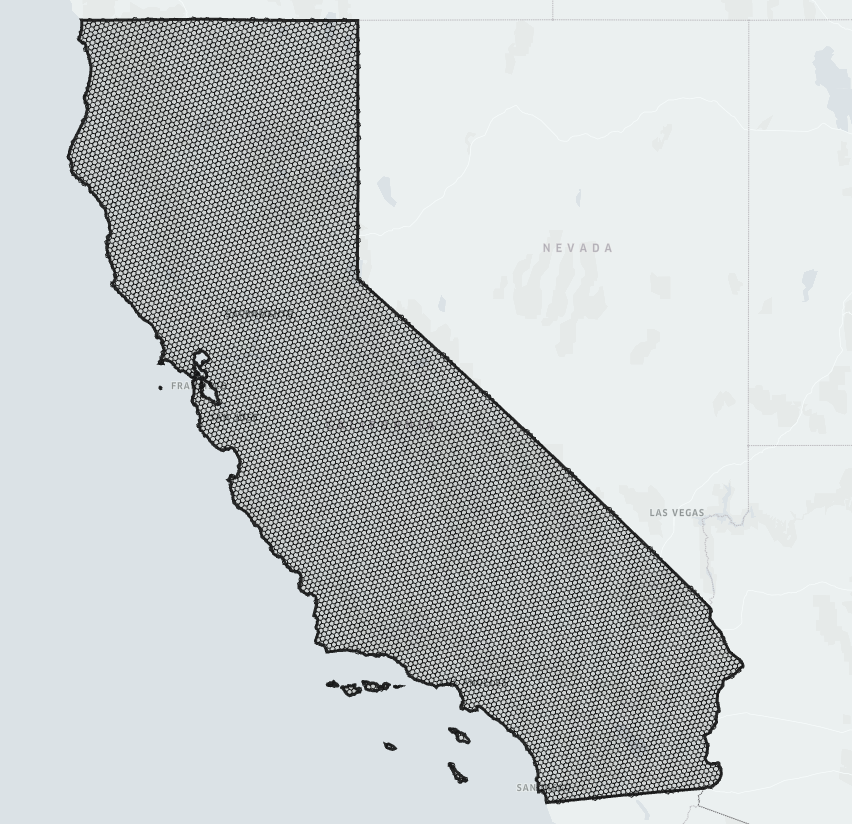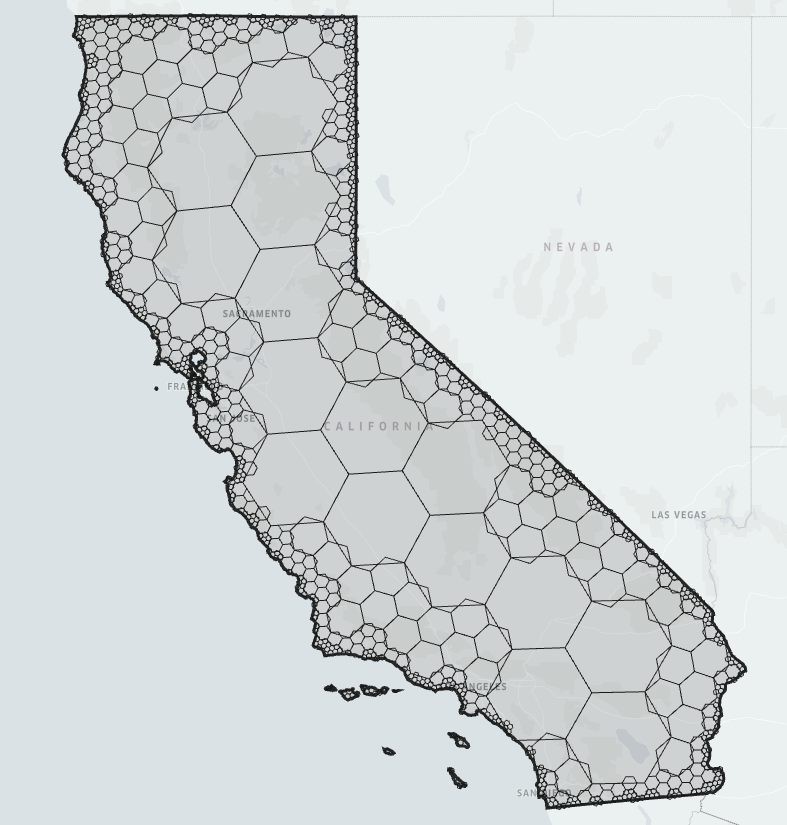California represented by 10633 uncompacted cellsCalifornia represented by 901 compacted cells

In use cases where exact boundaries are needed applications must take care to handle the hierarchical concerns. This can be done by taking care to use the hierarchy as a logical one rather than geographic. Another useful approach is using the grid system as an optimization in addition to a more precise point-in-polygon check.